| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 깊이우선탐색
- 스택과 힙
- 파이썬
- 캐싱
- 이진탐색
- bineary search
- 알고리즘
- 파이썬 오류
- 딥러닝
- 멱등
- 코딩테스트
- 코테
- 지도학습
- 강화학습
- 자바
- 비지도학습
- 오버라이딩
- 딕셔너리
- 프로그래머스
- 해시
- Merge sort
- 코딩
- 머신러닝
- 파이썬 알고리즘
- 너비우선탐색
- rest api
- post
- HTTP
- 백준
- BOJ
- Today
- Total
chae._.chae
03. 과대적합, 과소적합과 규제 방법 본문
✔ 과대적합
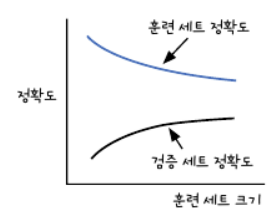
- 과대적합이란 모델이 훈련세트에서는 좋은 성능을 내지만 검증 세트에서는 낮은 성능을 내는 경우이다.
- 과대적합 모델 = 분산이 크다.
- 원인 : 훈련세트에 다양한 패턴의 샘플이 포함되지 않아서 검증세트에 적응하지 못해 성능이 낮음
- 해결 : 더 많은 훈련 샘플을 모아 훈련시킨다.
최적점 이후에도 훈련세트로 모델을 학습시키면 모델이 훈련세트에 밀착하여 학습하기에, 모델이 과대적합된다.
과대적합의 경우, 모델이 훈련세트에 집착하지 않도록 가중치를 제한할 수 있다.
(= 모델의 복잡도를 낮춘다)
✔ 과소적합
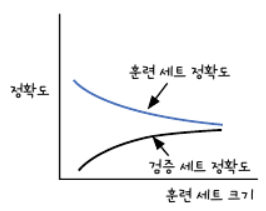
- 과소적합이란 훈련세트와 검증세트의 성능에는 차이가 크지 않지만, 모두 낮은 성능을 내는 경우
- 측정한 성능의 간격은 점점 가까워지지만, 성능 자체가 낮음
- 과소적합 모델 = 편향이 크다.
- 원인 : 모델이 충분이 복잡하지 않아 훈련 데이터에 있는 패턴을 모두 잡아내지 못함
- 해결 : 복잡도가 더 높은 모델을 사용하거나, 가중치의 규제를 완화.
* 모델복잡도 : 모델이 가진 학습 가능한 가중치의 갯수.
✔ 편향-분산 트레이드오프
- 편향을 줄이면(훈련세트의 성능 up), 분산이 커짐(검증세트와의 성능 차이 up)
- 분산을 줄이면 편향이 커짐
- 즉, 하나를 줄이면 하나가 커지는 관계이다. -> 분산/편향이 적절하도록 중간지점을 선택해야함
📖 규제방법
- 가중치 규제(regulation) : 가중치의 값이 커지지 않도록 제한하는 기법이다.
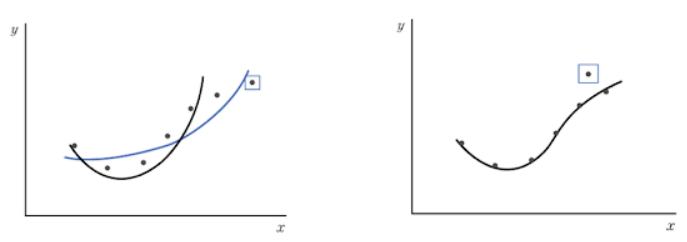
그래프의 성능을 평가할 때는, 경사가 급한 그래프보다는 경사가 완만한 그래프가 성능이 좋다고 말한다.
오른쪽 그래프는 샘플 데이터에 너무 집착한 모습임.
- 새로운 데이터에 적응하지 못하므로 좋은 성능을 가졌다고 할 수 X
- 모델이 일반화되지 않았다.
- L1 규제, L2 규제 기법
⚡ L1 규제
- L1 규제는 손실함수에 가중치의 절댓값인 L1 norm을 추가한 것이다.
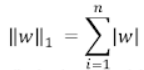
- norm에서의 n은 가중치의 갯수이므로, L1 규제는 가중치의 절댓값을 손실함수에 더한 것
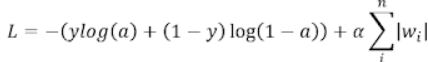
- alpha : L1 규제의 양을 조절하는 파라미터
- alpha값이 크면 규제가 강하다 => 전체 손실함수의 값이 커지지 않아지도록 w값의 합이 작아지게 됨
- alpha값이 작으면 규제가 약하다 => w의 합이 커져도 손실함수의 값이 큰 폭으로 변하지 않음
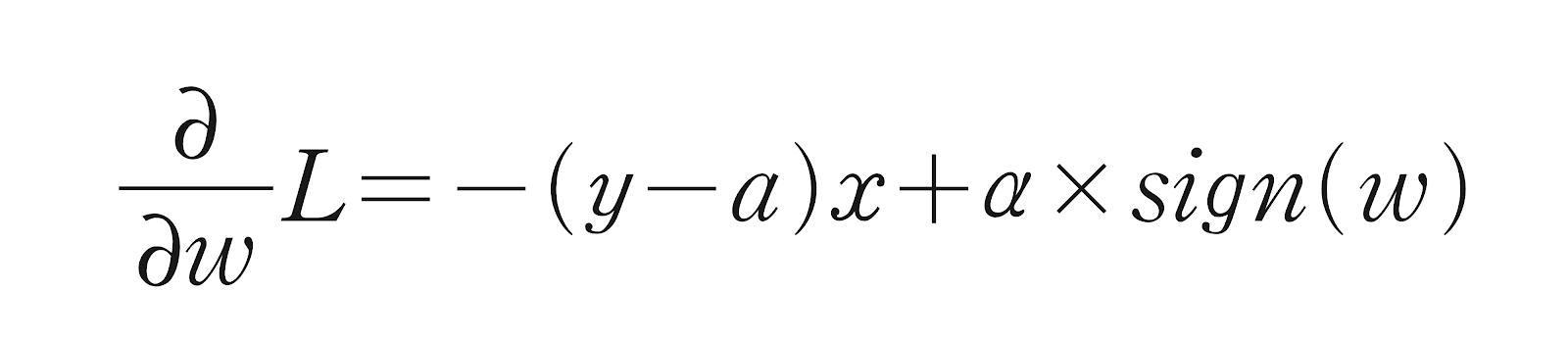
- w_grad += alpha * np.sign(w)로 나타낼 수 있다. // np.sign() : 부호를 반환
- 라쏘(Lasso)모델 : 선형회귀에 L1규제를 적용한 모델 (일부 가중치를 0으로 만들 수도 있음)
L1 규제는 규제 하이퍼파라미터 alpha에 많이 의존한다.
가중치의 크기에 따라 규제의 양이 변하지 않으므로 규제 효과가 좋다고 할 수 없다.
⚡ L2 규제
- L2 규제는 손실함수에 가중치에 대한 L2 norm의 제곱을 더한 것이다.
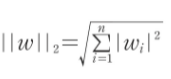
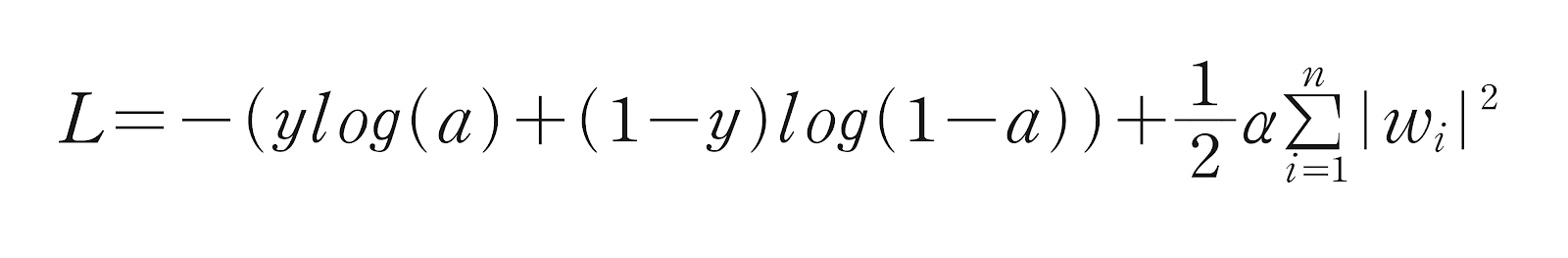
- alpha : 가중치의 양을 조절하는 하이퍼파라미터
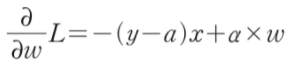
- w_grad += alpha * w 로 나타낼 수 있다.
- L2 규제는 그래디언트 계산에 가중치의 값 자체가 포함되므로, 가중치의 부호만으로 계산하는 L1 규제보다 더 효과적이다.
- L2 규제는 가중치를 완전히 0으로 만드는 경우는 없다. 가중치를 0으로 제외하면 특성을 제외하는 효과는 있지만 모델의 복잡도가 떨어진다. => L2 규제가 더 많이 쓰인다.
- 릿지(ridge)모델 : 회귀모델에 L2 규제를 적용한 모델
L1 규제와 L2 규제를 동시에 수행하는 경우도 있다.
L1 규제의 강도에 따라 모델의 학습 곡선과 가중치가 어떻게 변할까 ?
규제강도는 0.0001, 0.001, 0.01 세가지로 해보자.
l1_list = [0,0001, 0.001. 0,01]
for l1 in l1_list:
lyr = SingleLayer(l1=l1)
lyr.fit(x_train_scaled, y_train, x_va=x_val_scaled, y_val = y_val)
plt.plot(lyr.losses)
plt.plot(lyr.val_losses)
plt.title('Learning Curve (l1={}'.format(l1))
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.ylim(0, 0.3)
plt.show()
plt.plot(lyr.w, 'bo')
plt.title('Weight (l1={}'.format(l1))
plt.ylabel('value')
plt.xlabel('weight')
plt.ylim(-4, 4)
plt.show()

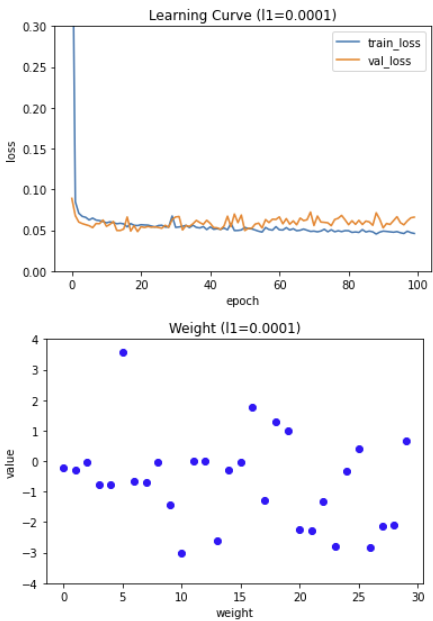

- 규제가 더 커질수록 훈련세트의 손실과 검증세트의 손실이 더 커진다. 즉, 과소적합 현상이 일어난다.
- 규제 강도가 커질수록 가중치 그래프의 값이 점점 0에 가까워진다.
- L2 규제도 L1규제와 비슷한 양상을 보이지만, L2 규제는 규제강도가 강해져도 L1만큼 과소적합이 심해지지는 않는다.
⚡교차검증(cross validation, k-폴드 교차 검증)
- 검증세트를 훈련세트에서 분리하느랴 훈련세트의 샘플 갯수가 줄어들어 모델을 훈련시킬 데이터가 부족해지는 경우 사용한다.
- 기존에는 전체 데이터세트를 8:2로 나누어 훈련세트와 데이터 세트를 얻고, 다시 훈련세트를 8:2로 나누어 훈련세트와 검증세트를 얻는 방법을 사용하였다.
- 교차 검증에서는 검증세트가 훈련세트에 포함된다.
- 교차 검증 방법
- 훈련세트를 모두 동일한 크기의 k개의 폴드로 나눈다.
- 첫 번째 폴드를 검증세트로 사용하고, 나머지 폴드를(k-1개) 훈련세트로 사용한다.
- 모델을 훈련시키고, 검증세트로 평가한다. 그 다음 폴드를 검증세트로 사용하며 모델훈련과 평가를 반복해준다.
- k개의 검증세트로 k번의 성능을 평가한 후, 성능의 평균을 내어 최종 성능을 구한다.
- k-폴드 교차 검증은 기존 방법보다 더 많은 데이터로 훈련할 수 있다.
k-폴드 교차 검증을 위한 반복문 코드
validation_scores = [] # 각 폴드의 검증 점수를 저장하기 위한 리스트
k = 10
bins = len(x_train_all) // k # bins갯수만큼 건너뛰며 폴드를 구분한다.
for i in range(k):
start = i*bins # 검증폴드 샘플의 시작과 끝 인덱스, 나머지가 훈련폴드 샘플의 인덱스임
end = (i+1)*bins
val_fold = x_train_all[start:end] # 검증폴드
val_target = y_train_all[start:end]
train_index = list(range(0, start))+list(range(end, len(x_train_all))) # 훈련폴드의 인덱스
train_fold = x_train_all[train_index] # 훈련폴드
train_target = y_train_all[train_index]
train_mean = np.mean(train_fold, axis=0) # 평균, 표준편차를 구해줌
train_std = np.std(train_fold, axis=0)
train_fold_scaled = (train_fold - train_mean) / train_std # 표준화 작업
val_fold_scaled = (val_fold - train_mean) / train_std
lyr = SingleLayer(l2=0.01)
lyr.fit(train_fold_scaled, train_target, epochs=50) # 훈련
score = lyr.score(val_fold_scaled, val_target) # 성능 검증
validation_scores.append(score)
print(np.mean(validation_scores)) # 평균값을 구해 최종성능을 계산한다.
- 훈련데이터의 표준화 전처리 작업을 폴드를 나눈 뒤에 수행 -> 폴드를 나누기 전에 표준화 전처리 작업을 한다면, 검증폴드의 정보가 새어나가기에 뒤에 해준다.
- 주로 직접 구현하기보다, 사이킷런의 model_selection 모듈에 교차검증하는 cross_validate()함수를 사용한다.
- 인자로 교차검증하고 싶은 모델의 객체, 훈련데이터, 타깃데이터를 전달하고, cv매개변수에 폴드 수를 지정하고 사용하면 된다. cross_validation()함수는 파이썬 딕셔너리를 반환한다.
⚡ Pipeline 클래스
- cross_validate()함수를 사용할 때에도 동일하게, 검증 폴더가 누설되면 안된다. 이때, 데이터를 전처리하는 과정에 Pipeline클래스가 사용된다.
- 사이킷런은 검증 폴더가 전처리 단계에서 누설되지 않도록 전처리 과정과 모델클래스를 연결해주는 Pipeline클래스를 제공한다.
- cross_validate()함수로 인자를 넘길때, Pipeline클래스로 감싸 전달해준다.
1. cross_validate()함수는 훈련세트를 훈련폴드와 검증폴드로 나누는 작업만 수행한다.
2. 전처리 단계와 SGDClassifie 클래스 객체의 호출은 Pipeline클래스에서 이루어진다.
3. 검증폴드가 전처리 단계에서 누설되지 않게 된다.
4. 사이킷런은 Pipeline함수를 만들어주는 make_pipeline()함수를 제공한다.
'ML > 딥러닝 입문' 카테고리의 다른 글
| 04. 다층 신경망 (0) | 2022.02.04 |
|---|---|
| 02. [로지스틱 회귀] 이진분류 (0) | 2022.01.13 |
| 01. [선형회귀] 수치 예측 (0) | 2022.01.10 |
